استكشاف متعمق لمفهوم tesseract، بدءًا من تعريفه الهندسي وحتى أهميته في الفيزياء، مع التركيز على استراتيجيات فهم هذا الشكل الغامض.

التسراكت هو كائن هندسي مشوش العلماء وعشاق العلم للأجيال. وفي هذه المقالة، سوف نلقي نظرة متعمقة على هذا المفهوم المثير للاهتمام، بدءًا من تعريفه وتاريخه وحتى تمثيله وتطبيقاته في الفيزياء. بالإضافة إلى ذلك، سوف نتناول التحديات نحن نواجه محاولة فهم هذا الأمر بشكل كامل الكائن متعدد الأبعاد.
ما هو تسراكت؟
يُطلق عليه أيضًا اسم tesseract مكعب, شكل هندسي مثير للاهتمام حقًا يظهر في بُعد يتجاوز تجربتنا اليومية. البعد الرابع. وعلى الرغم من أننا لا نستطيع رؤية هذا البعد الرابع بشكل مباشر، إلا أنه يمكننا محاولة فهمه من خلال التسراكت المقارنات والإسقاطات ثلاثية الأبعاد.
تخيل أننا في عالم ثنائي الأبعاد, مثل ورقة، ومحاولة فهم مكعب ثلاثي الأبعاد. ومن منظورنا ثنائي الأبعاد، يمكننا أن نرى فقط سلسلة من المربعات المتداخلة يتغير عندما يدور المكعب أو يتغير موضعه في عالمنا المسطح. وبالمثل، عند محاولة فهم تسراكت منا عالم ثلاثي الأبعاد, نرى أ خطة ثلاثية الأبعاد يتحول Tesseract ويتغير أثناء تحركنا الفضاء ثلاثي الأبعاد.
نظام التسراكتين تعقيد كبير ويتكون من عناصر تتصل وتترابط في شبكة متعددة الأبعاد. يحتوي tesseract على ثمانية رؤوس، وهي النقاط التي تلتقي فيها الحواف. تتم إضافة هذه الحواف المجموع 24، إنشاء نوع من الهيكل الذي يعطي الشكل للهيكل. بجانب، يحتوي التسراكت على 32 وجهًا مربعًا. الأسطح المسطحة التي تربط الحواف. وأخيراً يحتوي على 16 خلية مكعبة، مناطق ثلاثية الأبعاد تتشكل بين الوجوه المربعة.
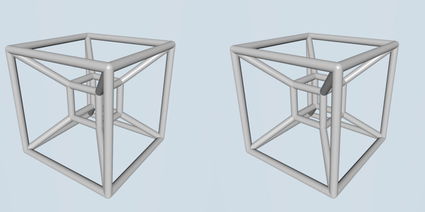
إن الكمال الهندسي للتسراكت وبنيته المعقدة متعددة الأبعاد يتحدى رؤيتنا ويذهل العقل الرياضي.
تاريخ مفهوم Tesseract
قصة تيسركت أ قصة رائعة ويغطي كلا من الرياضيات والخيال العلمي. لسنوات عديدة، هذا المفهوم لقد تطورت ويلتقط الخيال علماء الرياضيات والعلماء وكتاب الخيال العلمي على قدم المساواة.
تشارلز هوارد هينتون و”عالم جديد” (1888)
يعود أحد المعالم الأولى في تاريخ التسراكت إلى عام 1888 على يد عالم رياضيات بريطاني. تشارلز هوارد هينتون قدم مصطلح “tesseract” وبدأ في استكشاف خصائصه عمله هو “عالم جديد”. استخدم هينتون Tesseract أداة لاستكشاف البعد الرابع، تحدي التصورات التقليدية وفتح الباب أمام عالم جديد من الهندسة المزيد من الأبعاد.
مساهمات هنري بوانكاريه وماكس بروكنر
وفي العقود التالية، علماء الرياضيات مثل هنري بوانكاريه وماكس بروكنر لقد قدموا مساهمات كبيرة في دراسة التسراكت والأشياء ذات المكعب الفائق الأخرى. درس عالم الرياضيات الفرنسي الشهير بوانكاريه الخصائص الطوبولوجية للمكعبات الفائقة، أنشأها بروكنر، عالم الرياضيات الألماني النماذج الفيزيائية ثلاثية الأبعاد للمكعبات الفائقة لمساعدتك في دراستك.

ماري كوري وبوانكاريه يتحدثان في مؤتمر سولفاي عام 1911
Tesseract في الخيال العلمي
بالإضافة إلى وجوده في الرياضيات والهندسة، فإن التسراكت له مكانة بارزة. أدب الخيال العلمي. بدعة “”التجاعيد في الوقت المناسب”” قامت مادلين لينجل، التي نُشرت عام 1962، بنشر مفهوم التسراكت. آلية السفر عبر الزمكان بطريقة غير عادية. صنع عمل L'Engle ثقافة Tesseract الشعبية وساهم فيها الاعتراف في العقل العام.

ينقلنا فيلم “Interstellar” عبر “Tesseract”، وهو هيكل متعدد الأبعاد يتحدى فهمنا للزمان والمكان.
تصور وتمثيل tesseract
يعد تصور وتمثيل tesseract مهمة مثيرة للاهتمام لأنها وجوده في البعد الرابع بُعدًا يتجاوز تجربتنا اليومية القدرة على توجيه الإدراك. ومع ذلك، على مر السنين، طور علماء الرياضيات والعلماء أساليب إبداعية لمساعدتنا افهم هذا الكائن الهندسي الفريد جيدًا.
تمثيل ثنائي الأبعاد
إحدى الطرق الأكثر شيوعًا لتمثيل tesseract هي في عالمنا ثلاثي الأبعاد من خلال الإسقاطات ثنائية الأبعاد. تشبه هذه الإسقاطات الظلال أو الصور الظلية للتسراكت زوايا مختلفة. في كثير من الأحيان، يتم استخدام أنظمة الإحداثيات ثنائية الأبعاد لتمثيل الإسقاطات وإظهار كيفية تغير التسراكت. وعينا ثلاثي الأبعاد. توفر هذه التمثيلات ثنائية الأبعاد عرضًا مبسطًا لـ Tesseract ويمكن أن تساعد الطلاب على البدء. فهم بنيتها المعقدة.
توقعات تطلعية
هناك أسلوب شائع آخر وهو استخدام التوقعات الأمامية. ويشير يمثل tesseract في ثلاثة أبعاد، لكنه يؤكد على الخصائص التي تشير إلى وجوده في البعد الرابع. كما في الرسم الفني في الهندسة المعمارية, يمكن لهذه الإسقاطات تسليط الضوء على العلاقات المكانية وخصائص التسراكت بطريقة يمكن للبشر فهمها بسهولة. عقول ثلاثية الأبعاد.
الرسوم المتحركة والنماذج ثلاثية الأبعاد
من أجل فهم أعمق، يتم تطويرها الرسوم المتحركة والنماذج ثلاثية الأبعاد قطع. تسمح هذه الموارد للطلاب وعشاق العلوم بالتفاعل مع التسراكت الافتراضي ورؤية كيف يتغير ويتغير في أبعاد مختلفة. غالبًا ما يتم إنشاء نماذج ثلاثية الأبعاد برامج النمذجة ثلاثية الأبعاد, يمكن تدويرها واستكشافها من زوايا متعددة تمثيل ديناميكي وكامل لـ tesseract.

تسمح لنا نماذج tesseract ثلاثية الأبعاد برؤية عالم يتجاوز أبعادنا الثلاثة المعتادة، مما يتحدى تصورنا ويوسع حدود الفهم الهندسي والمكاني.
الواقع الافتراضي والمحاكاة
في عصر التكنولوجيا الحديثة والواقع الافتراضي و المحاكاة الحاسوبية يأخذ Tesseract التصور إلى مستوى جديد تمامًا. الناس يستطيعون انغمس في بيئات افتراضية ثلاثية الأبعاد تمثل تجربة tesseract والتفاعلية كيف تتكشف في البعد الرابع. أنه يوفر تجربة عميقة جداً ويساعد على فهم هذا الشكل الزائدي.

إن “تسراكت” والواقع الافتراضي هما مفهومان يغمراننا في أبعاد بديلة، أحدهما على المستوى النظري والآخر على المستوى التجريبي، مما يتحدى تصورنا للواقع.
تطبيقات في الفيزياء والعلوم
التسراكت، على الرغم من كونه مفهومًا هندسيًا في الأساس، إلا أن له حضورًا ملحوظًا فيه الفيزياء النظرية وعلم الكونيات. دورك في هذه المجالات ضروري استكشاف أبعاد إضافية في الكون وفهم البنية العميقة للزمكان.
نظرية الأوتار والأبعاد الإضافية
واحد التطبيقات تم العثور على أبرز جوانب التسراكت في نظرية الأوتار، وهو إطار نظري في الفيزياء يسعى إلى توحيد القوى الأساسية للكون. تقترح نظرية الأوتار أن هناك أبعادًا إضافية تتجاوز الأبعاد المكانية والزمانية الثلاثة التي ندركها. يتم تمثيل هذه الأبعاد الإضافية وفهمها بشكل أفضل كائنات مفرطة التكعيب مثل التسراكت. يتم استخدام tesseract كأداة مرئية ورياضية لوصف واستكشاف هذه الأمور الأبعاد المخفية فهم كيفية اهتزاز الأوتار، مما يؤثر على الخصائص الأساسية للمادة القوى في عالمنا.
النماذج الافتراضية والزمان والمكان
تلعب Tesseracts دورًا مهمًا في الخلق نماذج افتراضية في الفيزياء النظرية. في الزمكان ودراسته الهياكل المحتملة، تُستخدم المقطوعات كأشياء للدراسة لتمثيل التكوينات المعقدة للأبعاد والمنحنيات في الكون. هذه النماذج الافتراضية إنها تساعد الفيزيائيين على استكشاف إمكانية وجود أبعاد إضافية. الثقوب الدودية والأشكال الهندسية غير العادية هي الأكثر جرأة في الزمكان.

يدعونا التسراكت، في تمثيله ثلاثي الأبعاد، لاستكشاف أعماق الزمكان، ويكشف عن العلاقة المعقدة بين الهندسة والفيزياء الأساسية.
البحث العلمي ودراسة الكون
على الرغم من أن تمثيل واستكشاف التسراكت في البعد الرابع يمثل تحديًا، إلا أن بحث علمي استخدمت التمثيلات في نماذج ثلاثية الأبعاد ونماذج ثلاثية الأبعاد لفهم بعض جوانب الفيزياء بشكل أفضل. إنه ينطوي على استكشاف كيفية ظهور الأبعاد الخفية الجاذبية والطاقة المظلمة والظواهر الكونية الأخرى. توفر Tesseracts إطارًا مرئيًا ومفاهيميًا مفيدًا لمناقشة واستكشاف هذه النظريات والظواهر المعقدة.
للمهتمين لتعلم الرياضيات وانغمس في الفيزياء النظرية، فهناك موارد قيمة عبر الإنترنت مثل أفضل 9 صفحات لتعلم الرياضيات عبر الإنترنت. أساس متين للوصول إلى Tesseract وتطبيقاتها في الفيزياء.
ما هو تسراكت؟
التسراكت هو شكل هندسي ثلاثي الأبعاد يمتد إلى البعد الرابع، وغالبًا ما يتم تمثيله على شكل إسقاط ثلاثي الأبعاد لمكعب داخل مكعب آخر.